Before applying RSA, be sure to read all of the references first. Start here.

 

Not all tests will work well with Harpp-Hogan / Lertap RSA. The test should have at least 30 items, and an average score not greater than 80% of the maximum possible score.  The test items should use at least four options (true-false questions do not work well with Harpp-Hogan). Bad items, questions with negative discrimination, should be excluded from RSA. Items which have positive discrimination, but have one or more distractors with response proportions much greater than those for the correct answer, should be omitted.

 

The Stats1f figures (same as Stats2f in this case) show a reliability of 0.86 for this 60-item test.

 

 

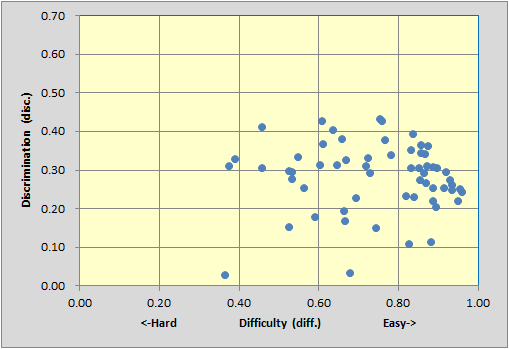
The test has a large number of easy items (diff. values above 0.80), which is often a characteristic of "mastery" tests. Nonetheless, there are five items with discriminations of 0.40 or greater, and also a fair smattering of items with discrimination in the 0.30 to 0.40 band. Not bad. (The two items whose blips are at the bottom of the scatterplot are P57 on the left, and P17 on the right. Both have disc. values below 0.05.)

 

 

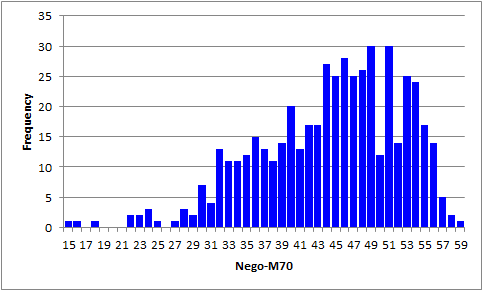
The score histogram has three stragglers on the left. We leave it to you to find out if the corresponding data records reveal a preponderance of strange answers -- blanks (unanswered questions), or asterisks (more than one answer selected by a student). (The M.Nursing sample shows how this can be done.)

 

When we ran Lertap's RSA option, Lertap paused twice, on P15 and P34. We told it to omit P15 but keep P34. Of these two items, P15 had a distractor selected by 45% of the students, quite a bit above the 37% for the correct answer. On P34, one distractor had 48%, with the correct answer at 46%, not much difference (these decisions to omit or keep items are a bit arbitrary -- both P15 and P34 had good discrimination; with 60 items and good reliability, the RSA results would probably have been about the same had P15 been retained for the analysis).

 

It doesn't make much sense to have Lertap run its RSA analysis with all of the scores. At the low end, say below 32 in this example, we might not be too concerned with cheating as, if it existed, it didn't do the students much good. At the high end, say above 52, there can't be many exact errors in common (EEIC), so students with these scores may as well be omitted. Running RSA with a low score of 32 and high score of 52 is what we decided on for this example.

 

 

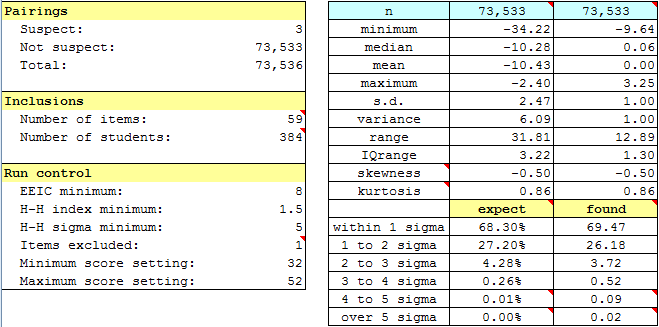
The RSAsig1 sheet shows that just 3 pairs were suspect, not many at all. (This is indicated above left, under the "Pairings" section.)

 

The "expect" and "found" results to the lower right are typical; ideally the values in these two columns will be very similar, more than what has resulted here -- the values on the left, "expect", are those found under a normal, or Gaussian, distribution; those on the right represent the values found in our sample.

 

 

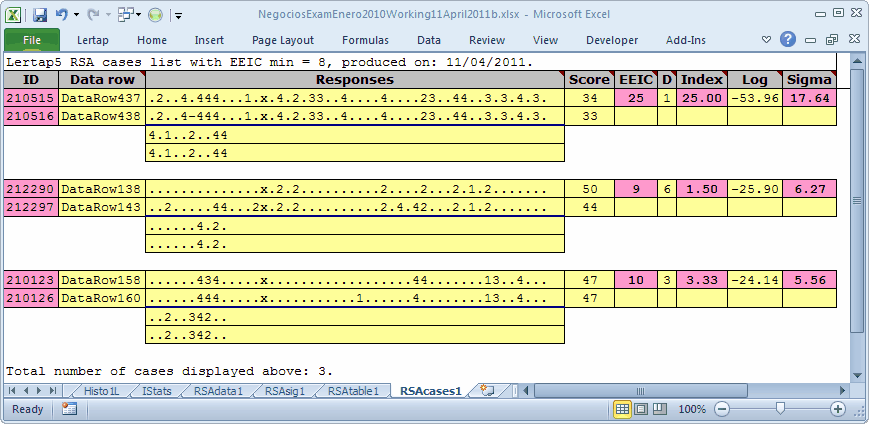
The RSAcases1 report reveals the identities of the 3 suspect pairs of students. Students 210515 and 210516 had only one response difference over the 60 items. On 25 of the questions, they chose exactly the same wrong answer (the same distractor). These two students were brothers, and, when invited in to "chat with the Dean", they admitted that they had cheated. For reasons unknown to us, the other two pairs of students were not challenged.

 

Moving on?

 

---

 

Tidbit:

 

There's much more to read about with regard to Lertap and its RSA analysis. Don't cheat yourself out of some top-flight reading. Start here.