Reliability and consistency

Coefficient alpha, eigenvalues, scree tests, omega reliability

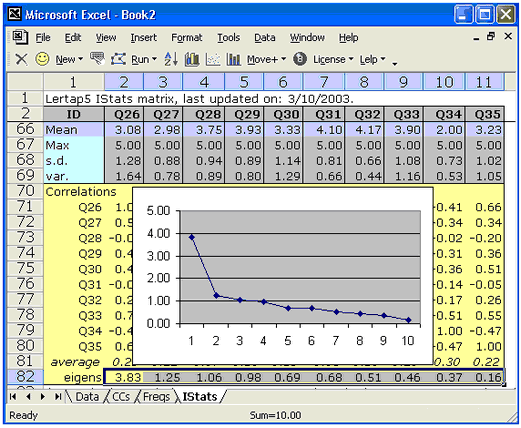
The plot below displays the eigenvalues from a ten-item rating scale (eigenvalues are also known as "latent roots").

The value of the first eigenvalue was almost 3.83, after which there is a sharp drop to the "scree" -- the second eigenvalue has a magnitude just a bit over 1.00 and from there on the eigenvalues decline in a regular, nearly linear manner. (Some researchers would accept this as an indicator of a "single-factor" scale.

There is an interesting, useful relationship between the magnitude of a test's or scale's first eigenvalue and coefficient alpha. This is discussed further in a technical paper.

A practical example based on using the first eigenvalue and its related eigenvector in the development of a rating scale is presented in this topic. Turn to Lelp (Lertap help) for more comments on eigenvalues, principal components, and how to get Lertap 5 to produce them.

Lertap 5 will form a complete inter-item correlation matrix, putting SMCs (squared-multiple correlation values) on the diagonal if wanted. Tetrachoric correlations may also be output. Comments on these options may be reviewed at this topic, and assistance with getting SPSS to pick up Lertap's correlation matrix is covered here.

An empirical comparison of alpha and coefficient omega, with more about eigenvalues and test reliability, is to be found in this research report.